Regions of Common Profile Models
The Regions of Common Profile (RCP) models are a type of ‘Mixture-of-Experts Models’ and try to describe how homogeneous groups of sites vary with the environment. This is done by grouping sites based on the biological content (species observed at each site) and determine how these groups vary across environmental or physical gradients (Foster et al. 2013). This approach assumes that assemblages of species at a site exists, and each assemblage can be described by its mean expectation of all species at that site. Within the the RCP model, these indicies are used to represent the data: sites as \(i = 1...n\), species as \(j = 1...S\) and groups as \(k = 1...K\) (we refer to these as RCPs). The model conditional expectation (given site membership) for all species is, \(\mathbb{E}(y_{ij}|z_{ik}=1)\). The model can be described as:
\[ \begin{equation} h[\mathbb{E}(y_{ij}|z_{ik})] = \alpha_j + X_i^\top\tau_j \tag{3}\label{eq:three} \end{equation} \]
Where \(\alpha_j\) is a species-specific intercept, \(Z_j^\top\) is a design matrix of covariates used to describe the RCPs. We can adjust the assemblage profile based on the species-wise expectation by incorporating a species wise covariates which can account for sampling artefacts. This extension was described in Foster et al. (2017).
\[ \begin{equation} h[\mathbb{E}(y_{ij}|z_{ik})] = \alpha_j + Z_i^\top\tau_j + W_i^\top\gamma_j + \nu_i \tag{4}\label{eq:four} \end{equation} \] Where \(W_i\) is a design matrix which represents covariates that could account for sampling biases in the observation of species at sites. Examples covariates to represent \(W_i\) might include the methods of collection of each sample or the time of day each sample was taken. These covariates then try and marginalize out observation difference of species at sites based on the input covariates, \(\gamma_j\) are species-specific parameters which describes these biases. Similar to the SAMs models any appropriate functional form can be used to describe the species-specific responses to physical environments or sampling artefacts. \(\nu_i\) is an offset which can be included to account between difference in sites specific survey effort (e.g. area survey). Any dispersion parameters, such as those for Negative Binomial, Tweedie or Gaussian model will also need to be estimated. \(z_i\) is an unobserved variable and is treated as a latent factor. The model assumes that \(z_i\) is the result of a multinomial sampling process with one trial and \(k x 1\) probability vector \(\pi_i\). The RCP model allows the RCP probability vector \(\pi_i\) to vary depending on the observation site’s position in environmental and geographical space. Where \(\pi_i=h(X_i)\), and \(X_i\) is the design matrix which contains the environmental and spatial covariates to describe site \(i\). \(h(.)\) is represented by a additive logistic function (Aitchison 1982) whose \(k\)th component is represented as:
\[ \begin{equation} \pi_{ik}\triangleq h(X_i,k)= \begin{cases} \frac{exp(X_i^\top\beta_k)}{1 + \sum_{m=1}^{K-1}\exp{X_i^\top\beta_{k'}}}, & \text{if $1 \leq k \leq K-1$,}\\ 1 + \sum_{m=1}^{K-1}\pi_{ik'}, & \text{if $k = K$,}\tag{5}\label{eq:five} \end{cases} \end{equation} \]
In this function \(\beta_k\) holds the parameter values for the \(k\)th linear combination which represents the environmental or physical covariates used to describe each RCP. The RCP model available for use in the ecomix package are comprised of the following three components. A model for RCP type which is described by the environmental and spatial covariates, a model for the expectation of each species’ observations with reference to the sampling approach or artefacts and a parametric model for how the observations vary around these mean species-specific expectations. RCP to date have largely been used for describing bioregions, ecoregions or assemblages classification for spatial management (Hill et al. 2017; Lyons et al. 2017). So this model can viewed as model-based bioregionalisation approach (Hill et al. 2020; Woolley et al. 2020). Where the probability of each RCP type occurring at each prediction point (site or prediction surface), represents a probabilistic distribution of an assemblage of species. These probabilities for each RCP can be directly assessed via equation 4.
Simulate Environmental Data
We generate a set of simulated environment predictors using Gaussian random fields with nugget effects on some of the variables.
library(raster)
library(RandomFields)
set.seed(007)
lenny <- 100
xSeq <- seq( from=0, to=1, length=lenny)
ySeq <- seq( from=0, to=1, length=lenny)
X <- expand.grid( x=xSeq, y=ySeq)
Mod1 <- RMgauss( var=1, scale=0.2) + RMnugget( var=0.01)
Mod2 <- RMgauss( var=1, scale=0.5) + RMnugget( var=0.01)
Mod3 <- RMgauss( var=1, scale=1)# + RMnugget( var=0.01)
Mod4 <- RMgauss( var=2, scale=0.1) + RMnugget( var=1)
simmy1 <- RFsimulate( Mod1, x=xSeq, y=ySeq)
simmy2 <- RFsimulate( Mod2, x=xSeq, y=ySeq)
simmy3 <- RFsimulate( Mod3, x=xSeq, y=ySeq)
simmy4 <- RFsimulate( Mod4, x=xSeq, y=ySeq)
X <- cbind( X, as.numeric( as.matrix( simmy1)), as.numeric( as.matrix( simmy2)),
as.numeric( as.matrix( simmy3)), as.numeric( as.matrix( simmy4)))
X[,-(1:2)] <- apply( X[,-(1:2)], 2, scale)
colnames( X) <- c("x","y","covar1","covar2","covar3","covar4")
env <- rasterFromXYZ( X)
names(env) <- c("Temperature", "Oxygen", "Depth", "Productivity")
env.df <- as.data.frame(env,xy=TRUE)
env_dat<-rasterToPoints(env)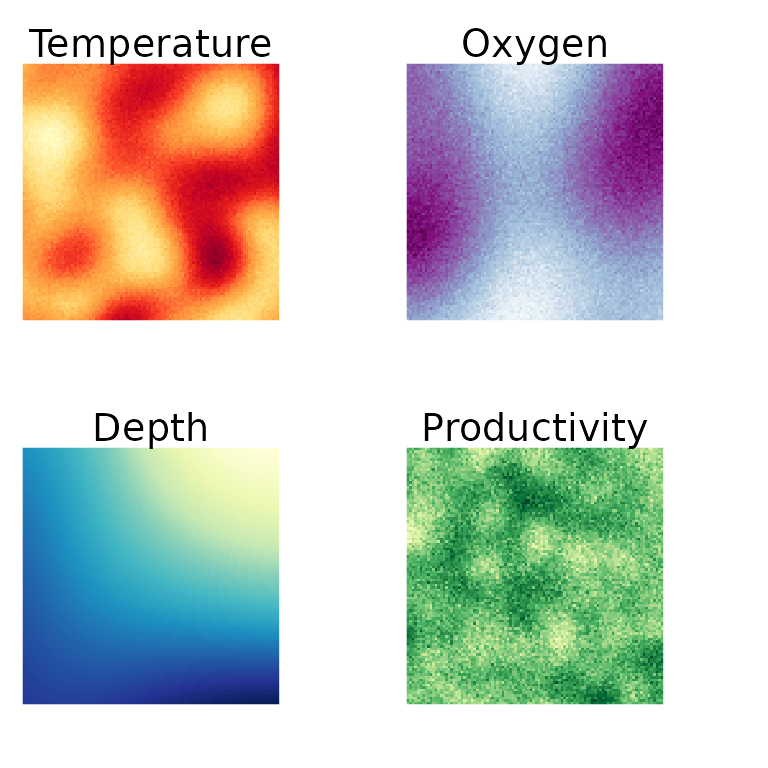
Figure 1. Simulated environmental variables used in Species Archetype Modelling
Model fitting
Due to the complex nature of the likelihood surface we need to use a multiple fitting approach to converge on the best model. This is computationally expensive for a big models, but it ensures that a detailed exploration of the model log-likelihood to help find the global maximum. We can use the regional_mix.multifit function to do this, this will return a list of models with nstarts as the number of starts to trying when searching the log-likelihood. Once we have run the multiple fits we select the ‘best’ models based on Bayesian Information Criteria (BIC), being aware that the ‘best’ model in both SAMs and RCPs can change dependent on the number of groups chosen and the functional for the covariates in the model. This is typically why we fit a full model with all the covariates and their expected functional form fixed and then we iterate thought \(k\) the number of groups. Once \(k\) is selected we could do model selection on the covariates with a fixed number of groups if so desired. Here we present a plot of the BIC values from a 100 fits per each of the model first for one to six RCPs (fig. 4a). We can that for these data and this covariate structure three RCPs appears to be the most parsimonious fit.